Решение задач из ЦТ по физике за 2012 г.

Подписывайтесь на нашу группу ВКонтакте https://vk.com/minskstudent и в FaceBook https://www.facebook.com/groups/7gran/ 

Оставляйте вопросы и комментарии внизу под статьей. Будем признательны за любые замечания и постараемся ответить на все вопросы.

Вариант 1

Часть В

 

Задача В1. Диаметр велосипедного колеса , число зубьев ведущей звездочки , ведомой ―  (см. рис.). Если велосипедист равномерно крутит педали с частотой , то модуль скорости v велосипеда равен …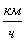 

 Решение.

Очевидно, скорость движения велосипеда равна скорости центра заднего колеса.

1. Пусть  ― угловая скорость вращения заднего колеса. Определим, как связана эта величина со скоростью движения центра . Для этого рассмотрим колесо с точки зрения инерциальной системы отсчета, движущейся со скоростью центра колеса 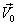 (см. рис.). В этой системе отсчета центр колеса покоится, а само колесо вращается с угловой скоростью , а значит точки, находящиеся на ободе колеса движутся по окружности с линейной скоростью , где  ― диаметр колеса. Эта скорость для заданной точки обода колеса направлена по касательной к окружности в рассматриваемой системе отсчета.

Для того, чтобы найти скорость любой точки колеса относительно земли необходимо воспользоваться законом сложения скоростей. На рисунке, например, показано, как найти скорость произвольной точки С обода колеса:

Применим этот же принцип и к точке касания колеса с поверхностью земли А:

В проекциях на ось Ox записанное векторное равенство примет вид:

Теперь очень важный момент! При качении колеса без проскальзывания по дороге (а именно такое качение мы предполагаем в данной задаче) точка А покоится относительно дороги, то есть .

Отсюда находим 

Все приведенные выше рассуждения были направлены как раз на получение выше записанной формулы. Заметим, что это не та привычная формула, которая связывает угловую скорость вращения и линейную скорость точек обода при движении по окружности. Полученная формула связывает линейную скорость центра колеса и угловую скорость его вращения, а вид этой формулы обусловлен именно отсутствием проскальзывания колеса.

2. Таким образом, для нахождения скорости движения велосипеда нужно узнать угловую скорость  колеса 2. Для нахождения этой скорости рассмотрим более подробно цепную передачу. Так как звездочка 2 жестко крепится к колесу, то за одно и то же время и звездочка и колесо поворачиваются на один и тот же угол, а значит угловые скорости звездочки и колеса совпадают.

Пусть  ― угловая скорость ведущей звездочки, тогда линейная скорость точек обода этой звездочки равна , где  ― радиус ведущей звездочки. Так как цепь, связывающая звездочки предполагается нерастяжимой, то линейная скорость точек обода второй звездочки равна линейной скорости точек обода первой:

где 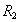 ― радиус ведомой звездочки.

Отношение радиусов звездочек можно найти, зная количество зубцов для каждой звездочки. Для этого заметим, что размеры (ширина) зубцов для обеих звездочек должны совпадать, так как размер паза в цепи для зацепления с зубом фиксирован и постоянен по всей длине цепи.

Пусть  ― ширина зуба. Запишем выражение для количества зубьев звездочки, находя его как отношение длины окружности к ширине зубца:

Отсюда находим

Тогда скорость велосипеда:

Остается только выразить угловую скорость ведущей звездочки через частоту вращения:

Тогда

Подставляем численные значения, не забыв перевести величины к СИ:

 Ответ: 12

 Примечание. Столь подробное решение задачи обусловлено желанием автора чему-то научить читателя. Непосредственно на тесте, обладая определенными навыками и опытом, многие обоснования можно опустить и решить данную задачу за 2-3 минуты.

 

Задача В2. К бруску массой , находящемуся на гладкой горизонтальной поверхности, прикреплена невесомая пружина жесткостью . Свободный конец пружины тянут в горизонтальном направлении так, что длина пружины остается постоянной (). Если длина пружины в недеформированном состоянии , то модуль ускорения a груза равен … .

 Решение.

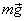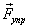Движение бруска происходит под действием сил тяжести , реакции опоры  и силы упругости  (см. рис.).

Под действием этих сил груз движется горизонтально с некоторым ускорением . Запишем для груза уравнение второго закона Ньютона:

.

Записанное уравнение спроектируем на ось :

 (проекции сил тяжести и реакции опоры равны нулю, так как эти силы перпендикулярны оси ).

Отсюда находим ускорение груза:

.

Сила упругости на основании закона Гука равна:

Тогда

Подставляем численные значения, не забывая переводить величины к основным единицам СИ:

Полученное значение не спешим записывать в бланк ответов, так как по условию ускорением необходимо найти в :

 Ответ: 20

 

Задача В3. На дне вертикального цилиндрического сосуда, радиус основания которого , неплотно прилегая ко дну, лежит кубик. Если масса кубика , а длина его стороны , то для того, чтобы кубик начал плавать, в сосуд нужно налить минимальный объем  воды , равный … .

 Решение.

На кубик действуют сила тяжести 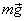 и сила реакции дна сосуда . Так как кубик прилегает ко дну неплотно, то в процессе наполнения сосуда водой кубик можно считать частично погруженным в жидкость, а значит, кроме указанных сил, на кубик будет действовать сила Архимеда .

Изначально кубик покоится, поэтому уравнение второго закона Ньютона для кубика имеет вид:

Спроектируем данное  уравнение на ось :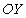

Запишем выражение для силы Архимеда:

, где  ― объем погруженной в жидкость части тела.

Пусть  ― высота воды в сосуде, тогда

Значит

Из записанного выражения видно, что с ростом  выталкивающая сила растет, а значит наступит момент, когда тело оторвется от дна и начнет всплывать. Сила реакции опоры при этом обратится в 0. Минимальному объему наливаемой жидкости соответствует ситуация, когда еще и ускорение равно нулю, поэтому уравнение второго закона Ньютона для случая начала плавания кубика примет вид:

Найдем объем воды, соответствующий этой высоте, не забывая учесть, что и сам кубик занимает некоторый объем:

Подставляем численные значения:

При вычислениях специально были проставлены размерности, что избавиться от необходимости делать перевод единиц.

 Ответ: 460

 

Задача В4. На невесомой нерастяжимой нити длиной  висит небольшой шар массой . Пуля массой , летящая горизонтально со скоростью  попадает в шар и застревает в нем. Если скорость пули была направлена вдоль диаметра шара, то шар совершит полный оборот по окружности в вертикальной плоскости при минимальном значении скорости  пули, равном … .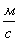

 Решение.

Пусть  ― скорость пули. Определим скорость шара с пулей после попадания. Для этого учтем, что при неупругом ударе выполняется закон сохранения импульса. В нашем случае на систему действуют внешние силы: тяжести и натяжения нити, которые перпендикулярны оси , то есть их проекция на эту ось равна нулю. Значит закон сохранения импульса выполняется в проекциях на ось .

Импульс системы до попадания равен: 

После попадания шар с застрявшим в нем пулей представляют собой единое тело массой . Пусть скорость этого тела равна . Тогда импульс системы после попадания равен:

На основании закона сохранения импульса можем записать:

Отсюда находим скорость шара с пулей после попадания:

Найдем условия, при которых шар способен совершить полный оборот по окружности. Для этого рассмотрим ситуацию, когда шар с пулей поднялись на некоторую высоту . Пусть эта высота больше длины нити (см. рис.).

Движение шара происходит под действием сил тяжести  и натяжения нити . Запишем уравнение второго закона Ньютона для шара:

Данное уравнение спроектируем на ось , которая расположена вдоль нити. При этом учтем, что, так как шар движется по окружности, то проекция полного ускорения  на выбранную ось представляет собой центростремительное ускорение:

Очевидно, радиус окружности, по которой движется шар равен длине нити 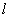, поэтому центростремительное ускорение шара равно:

Значения косинуса угла  находим из прямоугольного треугольника, изображенного на чертеже пунктиром:

Тогда уравнение второго закона Ньютона принимает вид:

Отсюда выразим силу натяжения нити:

Найдем скорость шара  на высоте . Для этого воспользуемся законом сохранения энергии. Отсчет потенциальной энергии будем вести от нижнего положения шара. Тогда в нижнем положении шар обладает только кинетической энергией:

Полная энергия шара на высоте  равна:

Сила натяжения нити перпендикулярна траектории движения шара, поэтому работы не производит, а значит для шара выполняется закон сохранения полной механической энергии:

Получаем окончательное выражение для силы натяжения нити:

Из полученного выражения видно, что с ростом высоты натяжение нити падает. В то же время, для движения шарика по окружности нить должна быть постоянно натянутой, так как при исчезновении силы натяжения движение шарика будет происходить только под действием силы тяжести, а такое движение, как известно, происходит по параболической траектории.

Таким образом, для движения шарика по окружности необходимо, чтобы минимальное значение силы натяжения нити, которое достигается в верхней точке траектории при , было больше нуля (в крайнем случае обращалось в ноль в этой точке:

Из полученного соотношения очевидно, что минимальное значение скорости пули, при котором шарика совершит оборот по окружности, составляет:

 Ответ: 200

 

Задача В5. Идеальный одноатомный газ, начальный объем которого , а количество вещества остается постоянным, находится под давлением . Газ охлаждают сначала изобарно, а затем продолжают охлаждение при постоянном объеме до давления . Если при переходе из начального состояния в конечное газ отдает количество теплоты , то его объем 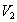 в конечном состоянии равен … .

 Решение.

Изобразим процесс, происходящий с газом на  диаграмме.

Запишем для газа уравнение первого начала термодинамики:

Знак "-" перед  обусловлен тем, что по условию газ отдает количество теплоты.

Изменение внутренней энергии  газа найдем как разность энергий между точками 1 и 3:

На основании уравнения Менделеева-Клапейрона, примененного к состояниям 1 и 3 газа получим:

Тогда

Работу газ совершает только на участке 1-2, так как на участке 2-3 объем постоянен, поэтому

Тогда

Подставляем численные значения:

 Ответ: 5

 

Задача В6. Два однородных кубика (см. рис.), изготовленных из одинакового материла, привели в контакт. Если начальная температура первого кубика , а второго ― , то при отсутствии теплообмена с окружающей средой установившаяся температура  кубиков равна … .

 Решение.

Пусть  ― удельная теплоемкость материала, из которого изготовлены кубики, а  ― плотность этого материала.

После соприкосновения кубиков, произойдет выравнивание их температур до некоторого значения , при этом кубик 2, температура которого выше отдаст количество теплоты:

,

а кубик 1 получит количество теплоты:

.

Так как теплообмен с окружающей средой отсутствует, то все количество теплоты, отданное кубиком 2 идет на нагревание кубика 1, поэтому должны выполняться условие:

Массы кубиков выразим через их объем и плотность:

Тогда

Для нахождения отношений объемов кубиков используем рисунок к задаче.

Пусть  ― условный размер одной клеточки рисунка. Тогда объем первого кубика:

,

а объем второго кубика:

.

Тогда отношение объемов: 

Значит,

В ответ по условия теста нужно записать целое число, округленное по правилам, т.е. 65.

Ответ: 65

 

Задача В7. На рисунке изображен график зависимости температуры  холодильника тепловой машины, работающей по циклу Карно, от времени 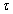. Если температура нагревателя тепловой машины , то максимальный коэффициент полезного действия  машины был равен … %.

Решение.

Запишем выражение для КПД тепловой машины. работающей по циклу Карно:

Из записанного выражения видно, что при постоянной температуре нагревателя КПД тепловой машины будет максимальным, если температура холодильника  минимальна.

Как видно из графика, минимальное значение температуры холодильника составляет .

Температуру нагревателя переведем в Кельвины:

Тогда максимальное значение КПД тепловой машины равно:

Ответ: 70

 

Задача В8. Четыре точечных заряда , ,  и  расположены в вакууме на одной прямой (см. рис.). Если расстояние между соседними зарядами , то в точке А, находящейся на этой прямой на расстоянии 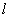 от заряда , модуль напряженности  электростатического поля системы зарядов равен … .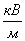

 

Решение.

Каждый заряд создает в окружающем пространстве электростатическое поле, напряженность которого на расстоянии  от заряда равна:

, где ,  ― модуль заряда.

Вектор напряженности  направлен вдоль прямой, соединяющей заряд и рассматриваемую точку пространства, при этом, если заряд положителен то вектор  направлен от заряда, а если отрицателен, то к заряду.

Если поле в точке А создается несколькими зарядами, то для вычисления напряженности этого поля применяют принцип суперпозиции.

Изобразим векторы напряженностей полей, создаваемых зарядами .

Так как все эти векторы направлены вдоль прямой, на которой расположены сами заряды и точка А, то для нахождения результирующей напряженности удобно ввести ось , совпадающую с указанной прямой и найти проекцию результирующей напряженности на эту ось:

В записанном выражении под  подразумеваются модули зарядов.

Подставляем численные значения:

Знак "-" в ответе показывает, что вектор  направлен противоположно направлению оси.

По условию необходимо было найти модуль напряженности:

 Ответ: 18

 

Задача В9. Аккумулятор, ЭДС которого  и внутреннее сопротивление , замкнут нихромовым  проводником массой . Если на нагревание проводника расходуется  выделяемой в проводнике энергии, то максимально возможное изменение температуры  проводника за промежуток времени  равно … К.

 Решение.

Изобразим схему включения нихромового проводника. Пусть  ― сопротивление проводника.

Ток в цепи находим по закону Ома для полной цепи:

Тогда в проводнике выделяется мощность:

 

.

За время 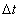 в проводнике выделится количество теплоты, равное:

.

Согласно условию на нагревание проводника идет  часть этой энергии:

Зная удельную теплоемкость нихрома и массу проводника, можем определить изменение температуры проводника:

.

Из записанного выражения видно, что изменение температуры проводника зависит от его сопротивления . По условию задачи нужно найти максимально возможное изменение температуры проводника. Для этого нужно найти максимальное значение записанного выше выражения.

Задача состоит в том, чтобы найти максимальное значение полученного выражения. От  здесь зависит только знаменатель, причем его часть, равная . Мощность будет максимальной тогда, когда данная часть будет минимальной.

Для того, чтобы исследовать данное выражение на минимум обычно используют понятие производной, однако, в школе производную теперь не проходят, поэтому укажем другой способ решения. Для этого вспомним неравенство Коши, которое состоит в том, что среднее арифметическое нескольких положительных числе всегда больше или равно их среднему геометрическому. Для двух чисел  и  это неравенство можно записать так:

, причем равенство возможно только при 

В исследуемом выражении положим , тогда неравенство примет вид:

Таким образом,

Подставляем численные значения:

 Ответ: 20

 

Задача В10. Проволочное кольцо радиусом  и массой , изготовленное из проводника сопротивлением , находится в неоднородном магнитном поле, проекция индукции которого на ось  имеет вид , где ,  ― координата. В направлении оси  кольцу ударом сообщили скорость, модуль которой . Если плоскость кольца во время движения была перпендикулярна оси , то до остановки кольцо прошло расстояние , равное … см.

 Решение.

Наметим ход решения задачи. При движении кольца в магнитном поле происходит изменение магнитного потока через плоскость кольца, так как индукция поля зависит от координаты. Это приводит к возникновению ЭДС индукции в кольце и появлению в нем тока. На возникший в кольце ток со стороны магнитного поля действует сила Ампера, которая и приводит к остановке кольца. Опишем эти процессы более подробно.

Пусть кольцо в некоторый момент движется со скоростью  и находится в точке с координатой . Через малый промежуток времени кольцо переместится в точку с координатой . Изменение магнитного потока через плоскость кольца за это время составит:

Такое изменение магнитного потока вызовет, согласно закону Фарадея, возникновение ЭДС в кольце, величина которого равна:

ЭДС приводит к появлению тока в кольце, сила которого по закону Ома равна:

Этот ток направлен так, как показано на рисунке, чтобы своим магнитным полем компенсировать изменение магнитного потока через плоскость кольца (правило Ленца).

Откуда же берется сила, тормозящая кольцо? На первый взгляд кажется, что силы Ампера, действующие на различные элементы кольца, могут лишь сжать кольцо, но не затормозить его (см. рис.).

Причина возникновения указанной силы кроется в неоднородности поля. Подробное рассмотрение этого вопроса выходит за рамки школьного курса физики. Здесь отметим лишь, что природа магнитного поля такова, что линии индукции поля не могут быть прямолинейными, если модуль индукции изменяется по величине. А значит, в описанном в условии задачи магнитном поле, кроме составляющей  есть еще и радиальная составляющая. Именно ввиду наличия этой составляющей магнитного поля у силы Ампера существует составляющая, направленная вдоль оси . Именно эта составляющая силы Ампера и тормозит кольцо.

Избавиться от необходимости точного вычисления силы Ампера поможет теорема об изменении кинетической энергии. Для использования этой теоремы рассмотрим кольцо в некоторой точке с координатой . Пусть в этой точке кольцо имеет скорость 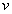.Через небольшой промежуток времени кольцо окажется в некоторой близкой точке, координата которой . Пусть скорость кольца в этот момент равна .

Определим изменение кинетической энергии кольца:

Так как изменение скорости мало, то квадратом величины  можем пренебречь. Тогда

Изменение кинетической энергии происходит за счет работы силы Ампера. Чтобы вычислить эту работу используем формулу:

, где  и  ― магнитный поток через плоскость кольца в точках  и  соответственно (влиянием собственного магнитного потока кольца пренебрегаем).

Такой подход позволяет избежать нахождения радиальной составляющей вектора магнитной индукции, так как магнитный поток зависит лишь от составляющей , перпендикулярной плоскости кольца.

Так как  и  малы, то ток в кольце на участке от  до  будем считать постоянным. Значение этого тока, согласно вышеприведенным рассуждениям равно:

.

Тогда

На основании теоремы об изменении кинетической энергии можем записать:

Полученное выражение связывает малое изменение скорости с малым изменением координаты. Из него, в частности, следует, что при увеличении координаты скорость уменьшается. Так коэффициент при  ―  не зависит ни от координаты, ни от скорости, то в полученном выражении можно произвести суммирование всех малых изменений координаты и скорости. В результате получим:

Подставляем численные значения:

 Ответ: 39

 

Задача В11. Напряжение на участке цепи изменяется по гармоническому закону (см. рис.). В момент времени  напряжение на участке цепи равно , а в момент времени  равно . Если разность напряжений , то действующее значение напряжения  равно … В.

 Решение.

По графику колебаний определяем период: . Так как в начальный момент значение напряжения равно амплитудному, то колебания происходят по закону косинуса с нулевой начальной фазой:

В записанном выражении время  подставляется в , а , как видно из графика – амплитудное значение напряжения.

Запишем выражение для разности напряжений в моменты времени  и :

Зная амплитудное значение напряжения, можно найти его действующее значение:

 

Ответ: 33.

 

Задача В12. На дифракционную решетку падает нормально параллельный пучок монохроматического света длиной волны . Если максимум второго порядка отклонен от перпендикуляра к решетке на угол , то каждый миллиметр решетки содержит число  штрихов, равное … .

 Решение.

Запишем условие максимумов для дифракционной решетки:

, где  ― период решетки,  ― порядок спектра.

Отсюда находим:

.

В нашем случае , поэтому период решетки равен:

Значит, 1 мм решетки содержит количество штрихов, равное:

 Ответ: 625.