Решение задач из ЦТ по математике за 2015 г.

Подписывайтесь на нашу группу ВКонтакте https://vk.com/minskstudent и в Facebook https://www.facebook.com/groups/7gran/

Оставляйте вопросы и комментарии внизу под статьей

Вариант 1

Часть В

Задача В1. Витя купил в магазине некоторое количество тетрадей, заплатив за них 24 тысячи рублей. Затем он обнаружил, что в другом магазине тетрадь стоит на 1 тысячу рублей меньше, поэтому, заплатив такую же сумму, он мог бы купить на 2 тетради больше. Сколько тетрадей купил Витя?

Решение.

Пусть x – количество тетрадей, купленных Витей.

Тогда цена одной тетради:  тыс. руб.

Значит, в другом магазине цена одной тетради: , так как тетради здесь дешевле на 1 тысячу рублей.

Так как в другом магазине Витя купил на 2 тетради больше за те же деньги, то

, то есть мы умножили новую цену на новое количество тетрадей и получили ту же самую сумму в 24 тысячи.

Решаем полученное уравнение:

Отрицательный корень не подходит, так как количество тетрадей должно быть положительным.

Таким образом, Витя купил 6 тетрадей.

Ответ: 6.

 

Задача В2. Найти наибольшее целое решение неравенства .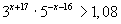

Решение.

Преобразуем неравенство таким образом, чтобы привести левую часть к одному основанию:

Так как основание под степенью меньше 1, то последнее неравенство эквивалентно следующему:

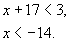
Наибольшее целое число из этого множества ― это -15.

Ответ: -15.

 

Задача В3. Найдите модуль разности наибольшего и наименьшего корней уравнения .

Решение.

Перенесем все слагаемые в левую часть и применим формулу разности квадратов:

Корни полученного уравнения: -3, -1, 1, 4.

Наибольший корень 4, а наименьший -3. Их разность равна 4 ― (-3) = 7.

Ответ: 7

Примечание: разложение квадратных трехчленов на множители подробно не расписывалось, так как предполагается, что решающим часть В это по силам. Если остались вопросы, то пишите комментарии в конце статьи – с удовольствием ответим на них.

 

Задача В4. Пусть ,  ― решения системы уравнений 

Найдите значение выражения .

Решение.

Будем решать данную систему уравнений методом подстановки:

 

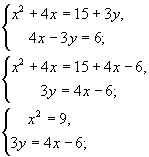
Из уравнения  следует, что .

При  получаем

При  получаем

Тогда значение искомого выражения:

.

Ответ: -24.

 

Задача В5. Найдите сумму корней (корень, если он единственный) уравнения

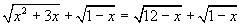
Решение.

Сначала определим ОДЗ для x. Для этого составим систему неравенств, руководствуясь тем, что подкоренные выражения должны быть неотрицательными:

Первое неравенство системы решаем методом интервалов:

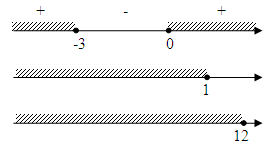
На рисунке изображены множества решений каждого из трех неравенств системы. Изобразим пересечение этих промежутков:

Таким образом,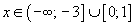 

Теперь приступаем к преобразованию исходного уравнения. Так как ОДЗ найдена, то можно смело проводить любые алгебраические преобразования с уравнением, не боясь появления посторонних корней (главное не забыть проверить полученные корни на принадлежность ОДЗ).

Казалось бы, одинаковые слагаемые в правой и левой части можно было убрать сразу, однако, это нельзя делать, так как наличие корня  влияет на ОДЗ уравнения.

Далее

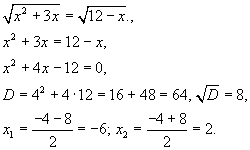
Второй корень не удовлетворяет ОДЗ, поэтому исходное уравнение имеет единственный корень -6.

Ответ: -6.

 

Задача В6. Найдите сумму целых решений неравенства .

Решение.

Данное неравенство удобно решать, используя метод интервалов. Для этого преобразуем исходное неравенство:

Заметьте, что, умножая на -1 левую и правую части неравенства, мы поменяли знак неравенства.

Далее разложим квадратный трехчлен в числителе на множители:

,

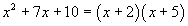а в знаменателе применим формулу разности квадратов:

.

Тогда неравенство принимает вид

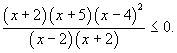
Все это были обычные шаги, необходимые для преобразования неравенства к виду, пригодному для применения метода интервалов.

Теперь внимание! Не спешите сокращать  в числителе и знаменателе. Так вы упустите из виду, что x не может быть равен -2. Перед сокращением необходимо пометить, что .

Итак, рассматриваем неравенство

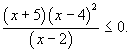
Расставляем нули числителя и знаменателя на числовой прямой, а также знаки неравенства, используя чередование знаков: начинаем со знака «+», а проходя через точку , знак не меняем.

Теперь наносим на полученную область решений выколотую точку  (на чередование знаков эта точка не влияет)

По полученной схеме записываем решение неравенства

.

Обратите внимание, что число 4 само по себе является решением неравенства, поэтому включается в множество решений.

Из записанного множества выписываем все целые решения: .

Их сумма равна -8.

​Ответ: -8.

 

Задача В7. Каждое боковое ребро четырехугольной пирамиды образует с ее высотой, равной , угол 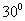. Основанием пирамиды является прямоугольник с углом  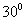между диагоналями. Найдите объем пирамиды V, в ответ запишите значение выражения .

 Решение.

Пусть SABCD – данная пирамида, а SO – ее высота.

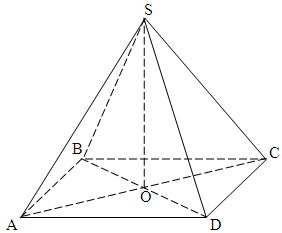
Рассмотрим треугольники SAO, SBO, SCO и SDO. Эти треугольники прямоугольные, так как SO – высота пирамиды, а значит, перпендикулярна любой прямой в плоскости (ABC). Катет SO – общий для всех четырех треугольников, а углы при вершине S у этих треугольников одинаковы по условию. Это значит, что указанные треугольники равны, а значит OA=OB=OC=OD. Таким образом, точка О равноудалена от вершин прямоугольника ABCD, то есть является точкой пересечения диагоналей прямоугольника.

Для нахождения объема пирамиды применим формулу:

, где  ― площадь основания, а H=SO – высота пирамиды.

По условию задачи .

Площадь основания можно найти по формуле площади четырех угольника:

, где  ― диагонали прямоугольника, а  ― угол между диагоналями.

Найдем половину диагонали прямоугольника. Для этого рассмотрим, например, треугольник SOA, для которого , .

Тогда

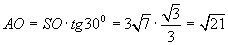
Значит диагонали прямоугольника

.

Тогда

.

Вычисляем объем пирамиды:

.

В ответ записываем число 

 Ответ: 147. 

 

Задача В8. Найдите (в градусах) наибольший отрицательный корень уравнения .

Решение.

Проще всего решить данную задачу можно, используя основное тригонометрическое тождество:

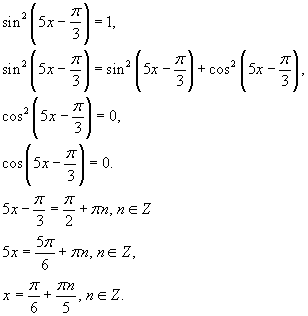
Очевидно, что при  соответствующий корень 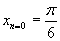 ― положительный, а уже при  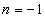получим .

Это и есть наибольший из отрицательный корней.

 Ответ: -6

 

Задача В9. Найдите количество корней уравнения .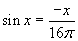

 Решение.

Очень похожая задача была в тесте за 2014 г. под номером В8.

Решить это уравнение аналитически невозможно, так как оно относится к классу трансцендентных уравнений. Однако для определения количества корней решение искать вовсе необязательно. Достаточно решить данное уравнение графически, то есть изобразить на координатной плоскости функции  и , найти точки их пересечения и подсчитать количество этих точек.

Функция 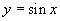 ― -периодическая функция, кроме того, значения этой функции лежат в интервале . В точке  функция принимает значение . Этого, в принципе, достаточно для построения схематического графика этой функции.

Функция  на координатной плоскости определяет прямую, проходящую через начало координат с отрицательным наклоном к оси абсцисс.:

Строим графики указанных функций в одной координатной плоскости:

Очевидно, что 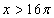при  и при 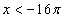, точек пересечения у графиков функций точно не будет, так как при указанных значениях , значения функции  по модулю превышают 1.

 Как видно из графика, заданные функции имеют 33 точки пересечения. Заметим, что задачу можно было решить, рассматривая лишь значения , так как функции, входящие в состав уравнения нечетные, а значит, их графики симметричны относительно начала ординат.

 Ответ: 33.

 

Задача В10. В прямоугольнике ABCD выбраны точки L на стороне BC и M на стороне AD так, что ALCМ – ромб. Найдите площадь этого ромба, если АВ=3, ВС=9.

 Решение.

Изобразим на чертеже описанный прямоугольник и обозначим на его сторонах точки L и M.

 

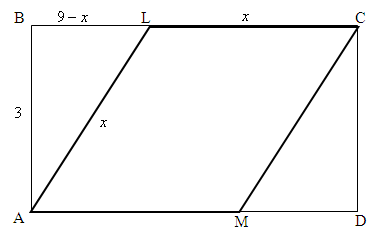
Пусть LC=x – сторона ромба, тогда AL=x, так как у ромба все стороны равны.

Рассмотрим прямоугольный треугольник ABL. У этого треугольника АВ=3, BL=9-x, AL=x.

Запишем для этого треугольника теорему Пифагора:

Таким образом, сторона ромба равна 5.

Высота ромба CD=BA=3/

Тогда площадь ромба:

 Ответ: 15.

 

Задача В11. Пусть .

Найдите значения выражения .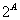

 Решение.

Преобразуем выражение, задающее А.

Сначала заметим, что 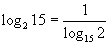, а это значит, что .

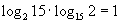Тогда

Здесь мы использовали формулу квадрата разности, а сначала сделали из двойки удвоенное произведение логарифмов, пользуясь замеченным выше свойством.

Далее

При раскрытии модуля в последнем выражении мы учли, что , а , поэтому разность под модулем положительная и знак модуля можно просто опустить.

Таким образом,

В последнем преобразовании мы внесли 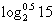в скобки слева и учли замеченное в самом начале свойство.

Далее, в первой скобке представим единицу как 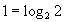 и воспользуемся формулой разности логарифмов:

В последнем выражении учтем, что

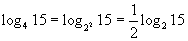
Тогда

Вычисляем искомое выражение:

.

 Ответ: 225.

 

Задача В12. Найдите сумму всех трехзначных чисел, которые при делении на 4 и на 6 дают в остатке 1, при делении на 9 дают в остатке 4.

 Решение.

Для того, чтобы решить задачу, нужно сначала найти какую-либо закономерность, которой подчиняются описанные в условии задачи числа, так как перебирать все трехзначные числа с указанными свойствами – не очень рациональная идея.

Для нахождения указанной закономерности заметим, что, например, числа, которые при делении на 4 дают в остатке 1 повторяются через 4, то есть образуют арифметическую прогрессию с разностью 4.

Действительно, число 5 при делении на 4 дает в остатке 1. Следующее такое число – 9, затем – 13, 17 и т.д.

Аналогично, числа которые при делении на 6 дают в остатке 1 повторяются через 6, например 13, 19, 25 и т.д.

А числа, которые при делении на 9 дают в остатке 4 повторяются через 9: 13, 22, 31 и т.д.

Теперь представим, что есть такое число, которое одновременно удовлетворяет всем трем свойствам, описанным в условии задачи, то есть при делении на 4 и на 6 дает в остатке 1, а при делении 9 дает в остатке 4. Одно из таких чисел, 13, очень просто находится методом подбора.

Если мы увеличим 13 на 4, то получим число 17. Это число будет при делении на 4 давать в остатке 1, однако остальные требования соблюдены не будут. Очевидно, что если мы увеличим число 13 на 36, то есть возьмем число 49, то это число будет обладать всеми свойствами, указанными в условии.

Число 36 одновременно делится на 4, на 6 и на 9, причем является наименьшим общим кратным этих чисел. Это значит, что все искомые числа образуют арифметическую прогрессию с разностью 36. Если за первый член такой прогрессии взять 13, то общий член можно записать в виде:

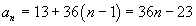
Так как число должно быть трехзначным, то

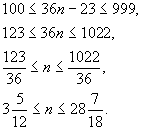
Так как n ― целое число, то n изменяется от 4 до 28. При данных n все члены найденной прогрессии – трехзначные числа. Всего этих чисел 25 (от 4 до 28 включительно).

Найдем сумму членов арифметической прогрессии с 4го по 28й:

.

 Ответ: 13825.

 

Подписывайтесь на нашу группу ВКонтакте https://vk.com/minskstudent и в Facebook https://www.facebook.com/groups/7gran/

Оставляйте вопросы и комментарии внизу под статьей