Решение задач из ЦТ по математике за 2017 г.

Подписывайтесь на нашу группу ВКонтакте https://vk.com/7grans и в Facebook https://www.facebook.com/7gran

Оставляйте вопросы и комментарии внизу под статьей

Вариант 1

Часть В

Задача В1. 

Для начала каждого из предложений А–В подберите его окончание 1–6 так, чтобы получилось верное утверждение

Начало предложения	Окончание предложения
А) Окружность с центром  точке (-8; -2) и радиусом 4 задается уравнением: Б) Уравнение прямой, проходящей через точку (-8; 2) и параллельной прямой , имеет вид: В) График обратной пропорциональности, проходящей через точку , задается уравнением:	1) xy = 2. 2) (x – 8)2 + (y – 2)2 = 4. 4) (x + 8)2 + (y + 2)2 = 16. 5) 4xy + 1 = 0. .

Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.

 

Решение.

А) Общее уравнение окружности имеет вид:

где (x₀; y₀) - координаты центра окружности, R – радиус окружности.

В нашем случае записываем:

Это соответствует варианту 4.

 

Б) У параллельных прямых угловые коэффициенты одинаковы, поэтому искомая прямая будет иметь уравнение вида:

Коэффициент b находим из условия прохождения прямой через точку (-8; 2):

Уравнение прямой имеет вид:

Это соответствует варианту 3.

 

В) Обратная пропорциональность – это функция вида:

где А – некоторый коэффициент.

Так как график обратной пропорциональности проходит через точку , то

Записываем уравнение обратной пропорциональности:

Это соответствует варианту 5.

Таким образом, в ответ следует записать А4Б3В5.

 

Ответ: А4Б3В5..

 

По всем вопросам, связанным с решением задачи, а также по вопросам репетиторства пишите автору, Антону Лебедеву.

 

Задача В2. Конфеты в коробки упаковываются рядами, причем количество конфет в каждом ряду на 4 больше, чем количество рядов. Дизайн коробки изменили, при этом добавили 2 ряда, а в каждом ряду добавили по 1 конфете. В результате количество конфет в коробке увеличилось на 25. Сколько конфет упаковывалось в коробку первоначально?

 

Решение.

Пусть x – количество конфет в каждом ряду при первом способе упаковки. Тогда (x – 4) – количество рядов. Таким образом, при первом способе упаковки в коробке содержится количество конфет, равное x(x – 4).

При втором способе упаковки количество конфет в ряду стало равным (x + 1), а количество рядов - (x – 2). Новое количество конфет: (x + 1) (x – 2).

Зная, что количество конфет увеличилось на 25, можем составить уравнение:

Таким образом, изначально в каждом ряду содержится по 9 конфет, количество рядов равно 5, а значит, количество конфет в коробке равно 45.

 

Заметим, что задачу можно было решать, используя т.н. маржинальный подход, то есть учесть только добавленные конфеты:

Понять записанное уравнение позволяет рисунок, где добавленные конфеты символически отмечены бордовым цветом.

 

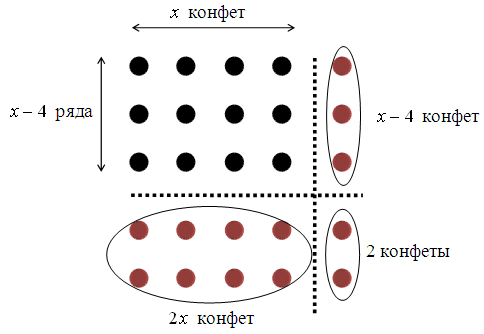
Ответ: 45.

 

По всем вопросам, связанным с решением задачи, а также по вопросам репетиторства пишите автору, Антону Лебедеву.

 

Задача В3. Известно, что при а, равном -2 и 4, значение выражения 4а³ + 3а² – ab + с равно нулю. Найдите значение выражения b + c.

 

Решение.

Подставим в выражение данные значения а и запишем соответствующие уравнения:

После преобразований получаем систему линейных уравнений:

Решаем полученную систему, вычитая из первого уравнения второе:

Тогда

 

Ответ: -34.

 

По всем вопросам, связанным с решением задачи, а также по вопросам репетиторства пишите автору, Антону Лебедеву.

 

Задача В4. Найдите произведение корней (корень, если он единственный) уравнения

 

Решение.

Данное уравнение удобно решать с помощью замены:

Тогда

Получаем уравнение для t:

Отрицательный корень отбрасываем, так как .

Тогда

Дискриминант полученного квадратного уравнения равен 133 > 0, поэтому уравнение имеет два корня, произведение которых по теореме Виета равно -27. Это число и нужно записать в ответ.

 

Замечания.

1. Абитуриенты практически всегда понимают, что подобные уравнения нужно решать с помощью замены, однако, выбирают не самую эффективную замену. Например, в данному уравнении многие пытаются использовать замену вида t = x² – 5x. Эта замена также приведёт к правильному ответу, но решение получится длиннее и будет связано с необходимость решать иррациональное уравнение.

2. Получив финальное квадратное уравнение, многие школьники пугаются того, что дискриминант в этом уравнении получается «некрасивым», то есть не является квадратом целого числа. Пугаться такой ситуации не нужно, так как теорема Виета помогает избежать операций с иррациональными корнями. Такие «ловушки» очень часто используются в заданиях ЦТ.

 

Ответ: -27.

 

По всем вопросам, связанным с решением задачи, а также по вопросам репетиторства пишите автору, Антону Лебедеву.

 

Задача В5. В параллелограмме с острым углом 45° точка пересечения диагоналей удалена от прямых, содержащих неравные стороны, на расстояния  и 2. Найдите площадь параллелограмма.

 

Решение.

Пусть ABCD – заданный параллелограмм, где . Проведём в параллелограмме диагонали AC и BD. О – точка пересечения диагоналей.

Из точки О опустим на сторону AD перпендикуляр OE, а на сторону AB перпендикуляр OK. По условию OE = 2, .

Проведем также высоты BF к стороне AD и CG к стороне AB.

Нетрудно заметить, что длина OE составляет половину длины высоты BF. Действительно, OE || BF, так как оба отрезка перпендикулярны AD, и BO = OD, так как диагонали параллелограмма точкой пересечения делятся пополам. Значит, OE – средняя линия ∆BFD и BF = 2OE = 4.

Аналогично .

Теперь можем найти сторону BC как гипотенузу прямоугольного треугольника ∆CGВ:

Площадь параллелограмма равна:

 

Ответ: 56.

 

По всем вопросам, связанным с решением задачи, а также по вопросам репетиторства пишите автору, Антону Лебедеву.

 

Задача В6. Пусть x₀ – наибольший корень уравнения , тогда значение выражения  равно … .

 

Решение.

Преобразуем исходное уравнение:

Вводим замену:

Тогда

Получаем два уравнения для x:

Нас интересует больший корень, поэтому x₀ = 2⁹.

Тогда

 

Заметим, что можно было решать и немного по-другому, расписав

и введя замену log₂x = t.. Суть решения от этого бы не изменилась.

 

Ответ: 56.

 

По всем вопросам, связанным с решением задачи, а также по вопросам репетиторства пишите автору, Антону Лебедеву.

 

Задача В7. Решите неравенство . В ответ запишите сумму целых решений, принадлежащих отрезку [-20; -2].

 

Решение.

Учтём, что .

Тогда неравенство принимает вид:

.

Так как основание , то исходное неравенство равносильно неравенству

Решаем полученное рациональное неравенство:

Применяем метод интервалов (см. рис.)

Записываем решение: .

На отрезке [-20; -2] лежат числа -7, -3, -2. Их сумма равна -12.

 

Ответ: -12.

 

По всем вопросам, связанным с решением задачи, а также по вопросам репетиторства пишите автору, Антону Лебедеву.

 

Задача В8. Найдите увеличенное в 9 раз произведение абсцисс точек пересечения прямой y = 12 и графика нечетной функции, которая определена на множестве  и при x  >  0 задается формулой .

 

Решение.

Нечётная функция – это такая функция, в которой при замене x на –x знак функции меняется на противоположный. Этот факт даёт нам возможность записать формулу для функции при x  <  0:

Давайте проверим, что записанное выражение действительно задаёт нашу нечётную функцию при x  <  0:

Найдем теперь точки пересечения графика этой функции с графиком функции y = 12. Для этого решим два уравнения:

1) При x  >  0 имеем:

Найденное значение нам подходит, так как .

2) При x  <  0 имеем:

Найденное значение нам подходит, так как .

Увеличенное в 9 раз произведение найденных значений равно:

 

Ответ: -143.

 

По всем вопросам, связанным с решением задачи, а также по вопросам репетиторства пишите автору, Антону Лебедеву.

 

Задача В9. Найдите площадь полной поверхности прямой треугольной призмы, описанной около шара, если площадь основания призмы равна 7,5.

 

Решение.

Пусть ABCA₁B₁C₁ – заданная прямая треугольная призма, в которую вписан шар.

Пусть r – радиус шара, а P – периметр основания призмы. Так как шар вписан в призму то окружность большого круга шара вписывается в основание призмы, а значит, площадь основания призмы:

С другой стороны, высота призмы равна диаметру шара: H = 2r.

Площадь полной поверхности призмы:

 

Ответ: 45.

 

По всем вопросам, связанным с решением задачи, а также по вопросам репетиторства пишите автору, Антону Лебедеву.

 

Задача В10. Найдите произведение наибольшего целого решения на количество целых решений неравенства

 

Решение.

Введем замену переменной

Тогда неравенство примет вид:

Знаменатель дроби в левой части неравенства всегда положителен, так как t неотрицательна, поэтому можем умножить обе части неравенства на 6 + t:

Полученное неравенство решаем методом интервалов, учитывая неотрицательность t.

Таким образом,

В данный интервал входят следующие целые решения: 23, 24, 25. Их количество равно 3, а наибольшее из них равно 25, поэтому в ответ записываем

 

Ответ: 75

 

По всем вопросам, связанным с решением задачи, а также по вопросам репетиторства пишите автору, Антону Лебедеву.

 

Задача В11. Первые члены арифметической и геометрической прогрессий одинаковы и равны 1, третьи члены также одинаковы, а вторые отличаются на 18. Найдите шестой член арифметической прогрессии, если все члены обеих прогрессий положительны.

 

Решение.

Пусть d – разность арифметической прогрессии, а q – знаменатель геометрической прогрессии.

Тогда три первых члена арифметической прогрессии:

1, 1 + d, 1 + 2d.

Три первых члена геометрической прогрессии:

1, q, q².

По условию задачи третьи члены обеих прогрессий равны между собой:

Вторые члены отличаются на 18. В условии не указано, в какую сторону отличие, поэтому рассмотрим оба варианта:

Таким образом, задача сводится к решению системы:

Решим полученную систему:

Квадратное уравнение из второй системы корней не имеет, так как его дискриминант отрицательный. Значит, остаётся одна система уравнений:

Знаменатель геометрической прогрессии не может быть отрицательным, ведь по условию все члены обеих прогрессий должны быть положительны, а значит, если бы знаменатель был равен -5, то второй член геометрической прогрессии был бы также равен -5.

Таким образом, q = 7, d = 24.

Тогда шестой член арифметической прогрессии:

 

Ответ: 121.

 

По всем вопросам, связанным с решением задачи, а также по вопросам репетиторства пишите автору, Антону Лебедеву.

 

Задача В12. ABCDA₁B₁C₁D₁ – прямая четырехугольная призма, объем которой равен 960. Основанием призмы является параллелограмм ABCD. Точки M и N принадлежат ребрам A₁D₁ и С₁D₁ так, что A₁M : A₁D₁ = 1 : 2, D₁N : NC₁ = 2 : 1. Отрезки A₁N и B₁M пересекаются в точке K. Найдите объем пирамиды SB₁KNC₁, если  и B₁S : SD = 3 : 1.

 

Решение.

Сделаем чертёж к условию задачи.

Обозначим стороны призмы как a, b, c, а угол при основании обозначим через α.

По условию задачи A₁M : A₁D₁ = 1 : 2, поэтому в нашим обозначениях

Далее, так как D₁N : NC₁ = 2 : 1, то

Кроме того, так как B₁S : SD = 3 : 1, то

.

Для вычисления объема пирамиды используем формулу:

где

S_осн – площадь основания пирамиды KNC₁B₁;

h – высота пирамиды.

Вычислим высоту пирамиды SE как расстояние от точки S до плоскости верхнего основания призмы.

Высота SE параллельна ребру DD₁, так как оба этих отрезка перпендикулярны плоскости верхнего основания (призма прямая). Точка S лежит на диагонали B₁D, значит, высота SE принадлежит диагональному сечению призмы.

Треугольники SEB₁ и DD₁B₁ подобны по двум углам, значит

Вычислим теперь площадь основания пирамиды. Это основание представляет из себя неправильный четырёхугольник, поэтому удобнее вычислить площадь основания, вычитая из площади параллелограмма площади треугольников:

Выразим площади, входящих в равенство фигур через стороны параллелограмма и угол α:

Для нахождения площади треугольника A₁KM сделаем дополнительное построение: из точки N проведем прямую, параллельную B₁M до пересечения с продолжением стороны A₁D₁ в точке F.

Треугольник ∆D₁NF подобен треугольнику ∆A₁B₁M по двум углам. Отсюда

Рассмотрим треугольник ∆A₁NF.

Основание этого треугольника:

а высота:

Тогда площадь треугольника:

Треугольники ∆A₁KM и ∆A₁NF с коэффициентом подобия:

Тогда площадь ∆A₁KM равна:

Тогда площадь основания пирамиды равна:

Объем пирамиды:

Но  - это объем призмы. Тогда

 

Ответ: 115.

 

По всем вопросам, связанным с решением задачи, а также по вопросам репетиторства пишите автору, Антону Лебедеву.